価格の最適化に関する論文の紹介: Price Investment using Prescriptive Analytics and Optimization in Retail

こんにちは．研究開発室の福井です．

現在，研究開発室ではリモートコミュニケーションと自動化をメインテーマとして研究開発を行っております．その中でも私は自動化の役に立ちそうな技術に関する研究を行っております．より詳細に言いますと，最近はオペレーションズ・リサーチ(OR)と呼ばれる分野に含まれるいくつかの問題に関して研究を行っています．今回の記事では，最近私が勉強中の価格の最適化に関する問題に関連した論文を紹介させていただきます．

今回は，KDD2020 で発表された以下の論文を紹介します．

Mehrotra, Prakhar, et al. "Price Investment using Prescriptive Analytics and Optimization in Retail." Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2020.

この論文では，Walmart(アメリカの大手スーパーマーケットチェーン)において実験的に利用されている，機械学習と OR (の数理計画問題)を用いて利益が最大化するような最適価格を推薦するシステム(Price Recommender System; PRS)について紹介されています．

はじめに
- 問題設定
- システムの構成
提案手法
システムのパフォーマンス評価
- 需要予測モデルの評価
- Live Price Investment Experiments
  - Analysis 1 (Dallas Market)
まとめ
最後に
参考文献

はじめに

Walmart の実店舗の運営において，以下の 2 点に関して意思決定を行う必要があります．

利用可能な予算の内，どの商品(アイテムまたは UPC)にどれだけの予算を割り当てるか?
それらの商品をどれくらいの価格で販売するか?

Walmart において，この 2 つの意思決定を行うプロセスは Price Investment と呼ばれています．また，Walmart では Every Day Low Price (EDLP) という戦略をとっており，一時的なプロモーションによる値下げではなく，日頃の価格をできるだけ低く保って需要の増加を目指しています．

問題設定

本研究の目的は Price Investment の問題を解き需要を最大化することにあります．膨大に存在するアイテムを整理するために，Walmart では階層的に商品のグループ分けを行っています．まずは department 単位で分類が行われ，さらに各 department 内の商品はカテゴリに分類されます．実際は，この下にさらなる分類の階層が存在するそうなのですが，今回はカテゴリによるグループ分けがメインとなります．

今回の研究では，Food & Consumables department 内のみで Price Investment タスクを解きます．このタスクを改めて記述すると以下の 2 つのフェーズから成ります．

全ての商品カテゴリ内で，最適な予算の割当を見つける(詳細は後述しますが，要は各カテゴリの商品に対してどれだけ費用を割いてどれだけの量を用意するかを決定します)
それぞれのカテゴリ内に含まれる各商品に関して最適な価格を推薦する

システムの構成

先述のフェーズ 1, 2 を解いて最適な価格を推薦するためのシステムは以下のような構成になっています．*1

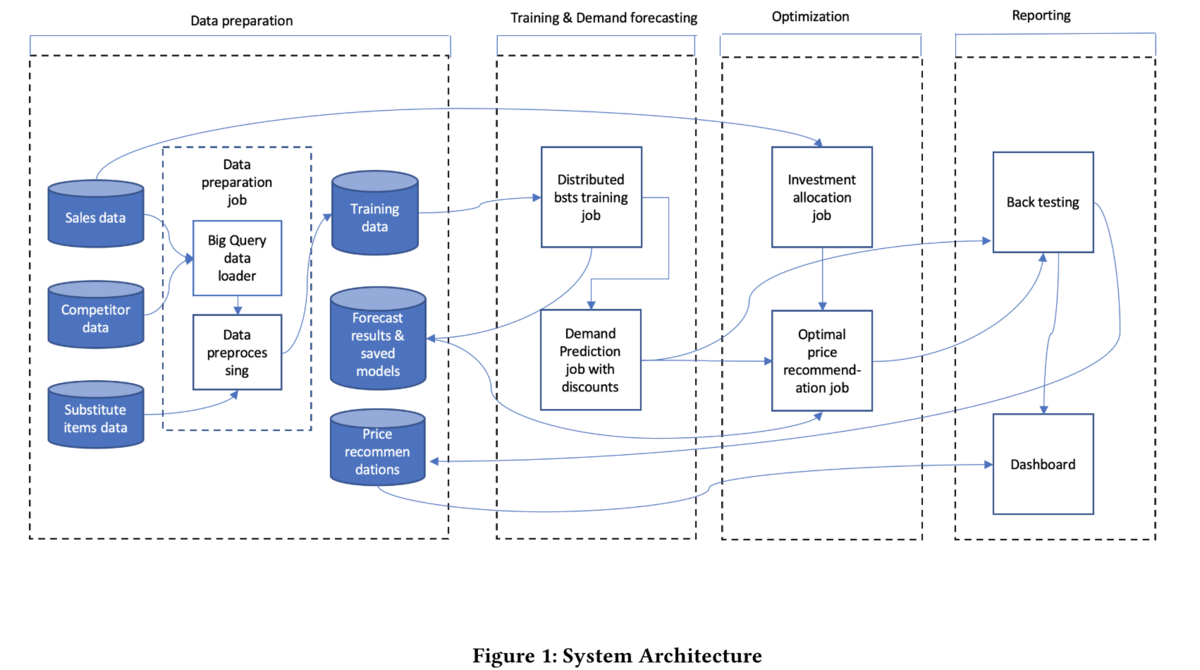
f:id:kazukifukui:20210323090651p:plain — Mehratora et al. 2012より

このシステムは左から順に以下のようなコンポーネントから構成されています．

Weekly-refreshed data loader: Walmart の直近の販売データをシステムに読み込みます
- 上図の各 data と Big Query の部分に該当します
Data pre-processor: データのクリーニングなどの前処理を行います
- 上図の Big Query の下にある Data preprocessing と Training data の部分に該当します
Model builder: 指定されたマーケット上の指定された商品に関する需要の予測を行います (フェーズ 1 の説明にて後述)
- 上図の Traing & Demand forecasting の部分に該当します
Portfolio optimizer: どの商品カテゴリにどれだけの予算を割り当てるか(investment)を最適化により決定します(フェーズ 1 の処理)
- 上図の Investment allocation job に該当します
Price optimizer: 各商品に対する設定価格の推薦を行います(フェーズ 2 の処理)
- 上図の Optimal price recommendation job に該当します
Post-assessment & Causal Inference Analysis: システムによる効果の評価を行います(評価実験に関するセクションにて後述)
- 上図の Reporting の部分に該当します

提案手法

使用するデータ

アメリカにある 4700 の Walmart の店舗を 52 のマーケットにグループ分けします．このグループ分けは顧客の買い物のパターンや地理的な情報に基づいて行われます*2．似た店舗間での価格の不一致が発生するのを避けるために，各商品の価格設定はマーケット毎に行います．これにより Walmart の店舗間でのカニバリゼーションを回避します．

Walmart における EDLP 戦略を実現するためにはマーケットの状況を把握する必要があり，最適な価格決定を行うために小売市場や競合他社に関する多様なデータを集められています．そして，これらのデータをどのくらいの粒度でモデルに落とし込むかを決定する必要があります(例えば以下のような点)．

時間: 需要予測を日，週，月もしくはより長いスパンのどの単位で行うか?
商品: 需要予測を各独立した商品ごとに行うか? それとも類似品やカテゴリ単位で行うか?
地理: 需要予測を各店舗毎に行うか? マーケット単位で行うか?

Walmart ではマーケット毎，四半期毎に価格の決定を行っているため，保有している粒度の細かいデータを集計して使用します．一方で，後述する需要予測のモデルに関しては，祝日などの短い期間内に発生するイベントの情報を利用するためにより短い週単位でマーケット毎にモデリングします．そして最適化時には，この週単位の予測をカテゴリ内のアイテムについて，また四半期内の全ての週について集計して最適化のモデルに入力します．

フェーズ 1: 予算の割当

ここでは，各商品カテゴリに対する予算の最適な割当(フェーズ 1)について説明します．このフェーズで決定された各カテゴリの予算に基づいて，フェーズ 2 では商品の最適な価格の推薦を行います．2 度目となりますが，価格の決定は四半期ごとに行います．実店舗の場合，EC サイトのように頻繁に値段を変更すると作業コストが高くなるためです．

各カテゴリに割り当てられる最適な予算は OR(の数理計画問題)によって導出されます．まずは，いくつか必要となる記号の定義を行います:

$C$ : 商品カテゴリの集合
$\mathcal{P}$ : カテゴリに適用できる価格の割引率(%単位)．有限個の割引率の中から各カテゴリに対する最適な割引率の割当を決定するという設定
$d^c_i \in {0, 1}$ : カテゴリに対する割引率の割当を決める決定変数．カテゴリ $c \in C$ に割引率 $i \in \mathcal{P}$ を設定するなら 1，そうでないなら 0
$V_{i,c}$ : カテゴリ $c$ に割引率 $i$ を設定した際の四半期における需要量の分布

また，需要量 $V_{i,c}$ を用いて以下の値を定義します(なお，数式の番号は論文のものと合わせてあります)．

$\displaystyle \begin{align} & \hat{V}_{i,c} := \text{Sample Avg. of } V_{i.c} \:\: \forall c \in C, \forall i \in \mathcal{P} \tag{2} \\ & \hat{R}_{i,c} := \hat{V}_{i,c} W_c \left(1-\frac{i}{100} \right) \tag{3} \\ & \hat{R}^\sigma_{i,c} := \text{Sample Var. of } V_{i,c} W_c \left(1-\frac{i}{100} \right) \tag{4} \\ & \hat{I}_{i,c} := \hat{V}_{i,c} O_c \tag{5} \end{align}$

ここで， $W_c, O_c$ は割引前のカテゴリの(ユニットあたりの)平均価格と平均コストで， $\hat{R}, \hat{I}$ は収益と出資の標本平均， $\hat{R}^\sigma$ は収益の標本分散となります*3．これに加えて，四半期内で達成した収益のターゲットの値を $\tilde{R} \in \mathbb{R}$ ，商品カテゴリ全体に対して利用可能な予算の合計を $B \in \mathbb{R}$ とします*4．

ここまでで必要な記号は揃いました．ここからは予算の最適な割当を決定する問題を定式化します*5．その定式化は以下のようになります．

$\displaystyle \begin{align} \min & \sum_{c \in C} \sum_{i \in \mathcal{P}} \hat{R}^\sigma_{i,c} d^c_i \tag{6a} \\ \text{s.t.} & \sum_{c \in C} \sum_{i \in \mathcal{P}} \hat{I}_{i,c} d^c_i \le B \tag{6b} \\ & \sum_{c \in C} \sum_{i \in \mathcal{P}} \hat{R}_{i,c} d^c_i \ge \tilde{R} \tag{6c} \\ & \sum_{i \in \mathcal{P}} d^c_i = 1 \:\: \forall c \in C \tag{6d} \\ & d^c_i \in \{0, 1\} \:\: \forall i,c \tag{6e} \end{align}$

上記の式の各行は以下のような意味を持ちます:

式 6a: これが上記の数理モデルの目的関数となります．ここでは，四半期内での収益のボラティリティを最小化するような商品カテゴリへの割引率の割り当て方を見つけます
式 6b: 商品カテゴリ $c$ への割引率 $i$ の割当(i.e. $d^c_i$ )を決定することにより，そのカテゴリに対する四半期内での平均需要 $\hat{V}_{i,c}$ が定まります．カテゴリの需要，つまりそのカテゴリが売れる量が決まることで，そのカテゴリに対する需要量だけを用意するのに必要なコスト(もしくは出資) $\hat{I}_{i,c}$ が定まります．この式では全カテゴリに関して発生するコストの合計が予算 $B$ を超えないよう制約を設定します
式 6c: カテゴリへの割引率の割当を決定するとそのカテゴリの需要量が定まり，(割引された後の)収益が定まります．この式では全カテゴリに関する収益の合計が目標値 $\tilde{R}$ 以上になるように制約を設定します
式 6d: 各商品カテゴリについて，設定される割引率がひとつのみであることを表します

上記の数理モデルは需要の分布の情報 $V_{i,c}$ に依存しています．より具体的には需要の平均と分散の情報が必要となりますが，次の節にてこの需要予測を行うモデル(価格と需要の関係を表すモデル)について説明します．

需要量の分布の推定

マーケット上のあるアイテムの需要量にはその価格だけではなく競合相手の価格や時期などの様々要素が影響します．論文内では Bayesian Structural Time Series (BSTS; Scott & Varian 2014)が利用されており，ベイズ推定を行うことで様々な要素を考慮した上での需要の分布の情報を得ることができます．

BSTS は名前の通りベイズによる時系列モデルであり，特徴選択，時系列予測，因果推論(Brodersen et al. 2015)等によく用いられるモデルです．BSTS は以下に示す observation equation (式 7)と transition equation (式 8)から成ります．

$\displaystyle \begin{align} Y_t &= Z^\top_t \alpha_t + \epsilon_t \tag{7} \\ \alpha_{t + 1} &= T_t \alpha_t + R_t \eta_t \tag{8} \end{align}$

Observation equation は観測値である $Y_t$ と潜在変数 $\alpha_t$ との関係を表し，一方 transition model は時間変化に伴う潜在変数 $\alpha_t$ の変化を表します．上記の BSTS の式は一般化して記された形であり $Z_t, T_t, R_t$ は structural parameter と呼ばれます．BSTS ではこの structural parameter を設定することで柔軟に様々な時系列データに対応する事ができます．具体的には，本研究では以下のような形のモデルとして設定されています.

$\displaystyle \begin{align} Y_t &= \mu_t + \tau_t + \beta^\top x_t + \epsilon_t,\: \epsilon_t \sim \mathcal{N}(0, \sigma^2_\epsilon) \tag{9a} \\ \mu_{t+1} &= \mu_t + \eta_t, \: \eta_t \sim \mathcal{N}(0, \sigma^2_\eta) \tag{9b} \\ \tau_{j,t+1} &= \tau_{j, t} \cos(\lambda_j) + \tau^\ast_{j,t} \sin(\lambda_j) + \omega_{j, t} \tag{9c} \\ \tau^\ast_{j,t+1} &= \tau^\ast_{j,t} \cos(\lambda_j) - \tau_{j,t} \sin(\lambda_j) + \omega^\ast_{j,t} \tag{9d} \\ \tau_t &= \sum^k_{j=1} \tau_{j,t} \tag{9e} \\ \lambda_j &= 2 \pi j/ s \tag{9f} \end{align}$

ここで潜在変数の $\mu_t$ はトレンド成分， $\tau_t$ は季節成分を表しています．式 9f の $s$ は最も長い季節成分のサイクルを表しており，式 9e にあるようにモデル内では $k$ 個の異なる周期が考慮されています．*6．

先にも軽く触れたように，各マーケットにおいてアイテム(商品)，週のレベルで上記の需要のモデリングが行われます．すなわち，式 9a の $Y_t$ は $t$ 番目の週に観測されたある(単一の)アイテムの需要量となります．そして，式 9a における特徴ベクトル $x_t$ は以下のような情報を含みます．

アイテムの現在の価格
競合他社における，その商品の週毎の平均価格
週毎の Walmart における価格と競合の価格との差
その週に Walmart が行った商品に関するプロモーション
その週に発生した祝日などのイベントの情報

この BSTS のモデル(実装は R の bsts パッケージ)に Walmart が保有するデータを入力することで，各アイテムの需要量の平均と分散が推定できます．ここで得られた結果をカテゴリ/四半期単位になるよう集計することでフェーズ 1 にて必要であった各カテゴリに対する需要量の平均と分散が得られます．

フェーズ 2: 商品(アイテム)毎の価格の最適化

フェーズ 2 では，フェーズ 1 の数理計画問題を解くことで得られた商品カテゴリ $c$ に対する予算の割当(investment)の量 $\tilde{I}_c$ を用いて，カテゴリ $c$ 内の各アイテムに対する最適な設定価格を計算します．まずは，必要となる記号を以下に定義します:

$\mathcal{M}_c$ : カテゴリ $c \in C$ に属するアイテム(商品)の集合
$\mathcal{P}_m$ : アイテム $m \in \mathcal{M}_c$ に設定可能な価格の集合
$\hat{R}_m(p_i)$ : アイテム $m$ に価格 $p_i$ を設定した場合の次の四半期の収益の推定値
$\hat{I}_m(p_i)$ : アイテム $m$ に価格 $p_i$ を設定した場合の次の四半期の出資(必要となるコスト)の推定値
$\hat{V}_m(p_i)$ : アイテム $m$ に価格 $p_i$ を設定した場合の次の四半期の需要量の推定値
$\tilde{V}_c$ : カテゴリ $c$ に属するアイテムの需要量の目標値

以上の記号を用いて，次の四半期における各商品の最適な価格を以下の数理最適化問題により算出します．*7 *8

$\displaystyle \begin{align} \max & \sum_{m \in \mathcal{M}_c} \sum_{p_i \in \mathcal{P}_m} \hat{R}_m(p_i) y^m_{p_i} \tag{10a} \\ \text{s.t.}\: & \sum_{p_i \in \mathcal{P}_m} y^m_{p_i} = 1 \:\: \forall m \in \mathcal{M}_c \tag{10b} \\ & \sum_{m \in \mathcal{M}_c} \sum_{p_i \in \mathcal{P}_m} \hat{I}_m (p_i)y^m_{p_i} \le \tilde{I}_c \tag{10c} \\ & \sum_{m \in \mathcal{M}_c} \sum_{p_i \in \mathcal{P}_m} \hat{V}_m(p_i) y^m_{p_i} \ge \tilde{V}_c \tag{10d} \\ & y^m_{p_i} \in \{0, 1\} \:\: \forall p_i \in \mathcal{P}_m, \forall m \in \mathcal{M} \tag{10*} \end{align}$

上記の式の各行は以下のような意味を持ちます:

式 10a: 数理計画問題の目的関数を表します．ここでは，次の四半期内での収益が最大化するようなアイテム $m$ の価格 $p_i \in \mathcal{P}_m$ を選択します
式 10b: アイテム $m$ に設定する価格は $\mathcal{P}_m$ の中の 1 つのみ
式 10c: カテゴリ $c$ 内のアイテムに対する出資の合計がフェーズ 1 で計算した予算の割当 $\tilde{I}_c$ を超えないように制約を設定
式 10d: 価格の設定により定まるカテゴリ内の需要の合計が目標値 $\tilde{V}_c$ 以上となるようにする
式 10*: $y^m_{p_i}$ は商品 $m \in \mathcal{M}$ に価格 $p_i \in \mathcal{P}_m$ を設定するなら 1，そうでないなら 0 を取る決定変数．最適化によりこの変数の値が決まります．

また，論文内では明記されていませんが上記の式 10a - 10d の他にもコスト，マージン，在庫等の様々なビジネスルールが価格の決定において考慮されているとのことです．そのようなルールの例として代替可能な商品の考慮があります．代替可能な商品によって発生するカニバリゼーションを回避するために Walmart 内では以下のようなビジネスルールを設定しています．

同じ line に属するアイテムは同じ価格を設定する*9
ladder product に関しては 1 つ辺りの価格が安くなるように設定する*10

システムのパフォーマンス評価

需要予測モデルの評価

まずは過去データを用いて需要予測モデルのバックテストを行います．テストに使用するデータは，過去における Walmart 内で実際に価格の補正が行われた 2 つの期間 (investment wave) における実際の需要量です．

下記の Table 1 がバックテストにおいてパフォーマンスが良かった上位 5 個の商品カテゴリに関する結果となります．ここでは，需要の増加量の実際の値(Actual pre. vs post 列)と予測値(Model pre. vs post 列)を Mean Absolute Percentage Error (MAPE)で比較しています．MAPE の列に示された結果からもわかるように，需要量の変化の予測値の誤差は 3%以内に収まっています．いつくかの商品カテゴリでは価格の変更により需要量が減少していますが，これらに関してはカテゴリに対する一般的な需要の低下によるものであることが追加調査で判明した旨が本文中に記載されています．

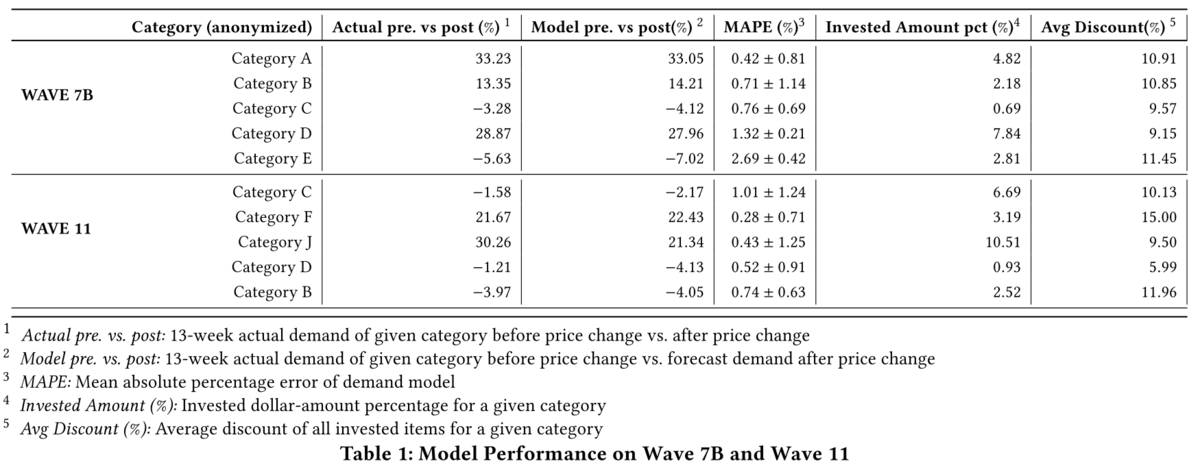
f:id:kazukifukui:20210323092601p:plain — Mehratora et al. 2012より引用

Live Price Investment Experiments

ここでは価格推薦システム(PRS)に基づいた価格変更の有効性の評価を行います．2019 年のある四半期中に 2 つのマーケット(500 店舗)の今回提案した PRS を用いて予算の割当と価格設定を行いました．評価では需要量予測の MAPE と価格変化による需要量への影響に着目します．より具体的には以下の点に着目します．

実際の需要量増加(lift)の前年比(YoY)
予測された需要量の増加の前年比
実測値と予測値の誤差(MAPE)
評価対象の 2 つのマーケットと似たマーケット(control price market)のデータ
- 後述する因果推論のみに評価を依存しないようにするため

また，価格変化の効果を評価するために R の bsts パッケージ(+ 明記されていませんが恐らくCausalImpact)の因果推論の機能を用いて検証が行われています．評価には A/B テストのような方法も考えられますが同一マーケット内の店舗間での価格の不一致によるカスタマーエクスペリエンスの悪化(加えて，それによる実験結果への影響)や実店舗における価格変更は作業コストが高くなるという点を踏まえて，A/B テストに替わり因果推論による評価方法が採用されています．*11

f:id:kazukifukui:20210323092615p:plain — Mehratora et al. 2012より引用

Table 2 ではパフォーマンスが良かった上位 5 つの商品カテゴリと Food & Consumables department 内の全カテゴリでの平均に関する結果が示されています．この表にあるように価格変更による需要量の前年比は control のそれよりも高くなっていることが分かります．

Analysis 1 (Dallas Market)

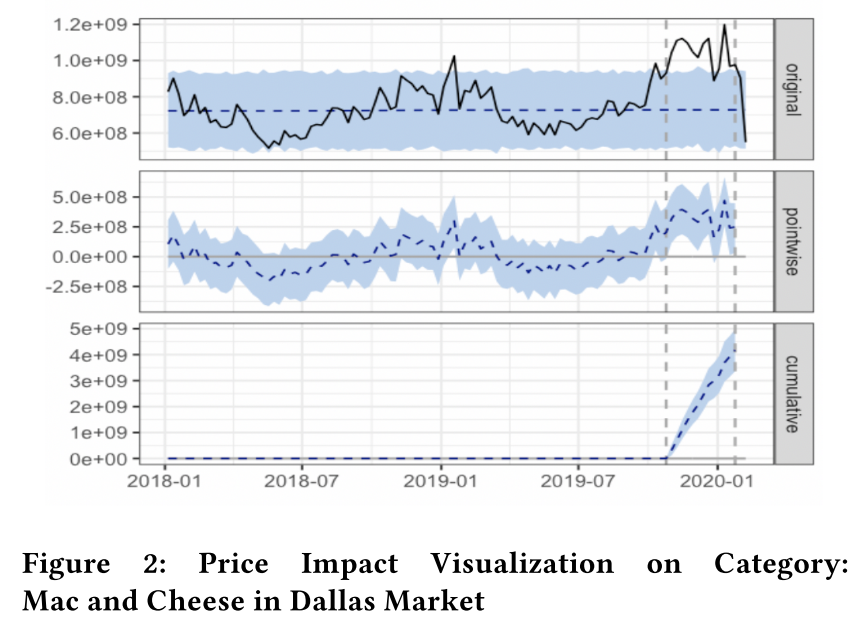
Figure 2 にあるように価格変更後の需要の実測値が平均 10.5B(個)である一方，価格変更を行わなかった場合の平均は 0.73B(95%信頼区間は[0.67B, 0.79B])と推定されており，価格変更により 0.32B(95%信頼区間は[0.26B, 0.38B])の効果があったと考えられます
価格変更後の実測値を合計すると 13.64B．また価格変更がなかった場合この値は 9.46B(95%信頼区間は[8.67B, 10.28B])と推定されます．

これらの結果より，介入(価格変更)による需要量が統計的に優位に増加したことが分かりました．また，論文内の Analysis 2 と Figure 3 ではもう 1 つのマーケット(Kansas City Market)に関する同様の分析が行われており，そちらにおいても価格変更による需要の増加が統計的に優位であったことが説明されています(似た結果のため，ここでは割愛します)．*12

f:id:kazukifukui:20210323092537p:plain — Mehratora et al. 2012より引用

まとめ

Walmart の Food & Consumables department において最適価格を算出するシステム(PRS)を提案しました
バックテストや live price investment experiments により，現在 Walmart で行われていた従来のルールベースの価格設定よりも高い有効性が確認できました
Future work としては，Walmart 内の全 department において今回のシステムの導入が検討されています

最後に

今回の論文紹介は以上となります．解説が長くなってしまいましたが最後まで読んでいただきありがとうございました．フレクトでは，今後もお客様にとって付加価値となるような新たな分野や技術に関して開拓を行っていきます．今回紹介した価格の最適化以外の OR の問題に関しても積極的に研究を行っているため，もしご興味がありましたら是非ご相談ください．

参考文献

Mehrotra, Prakhar, et al. "Price Investment using Prescriptive Analytics and Optimization in Retail." Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2020.
Scott, Steven L., and Hal R. Varian. "Predicting the present with Bayesian structural time series." International Journal of Mathematical Modelling and Numerical Optimisation 5.1-2 (2014): 4-23.
Brodersen, Kay H., et al. "Inferring causal impact using Bayesian structural time-series models." Annals of Applied Statistics 9.1 (2015): 247-274.

*1:システムのスケーラビリティに関する説明が論文の 3.3 にて行われていますが，今回の論文紹介では割愛します．

*2:マーケットに関する詳細は説明されていませんが，評価実験において Dallas Market や Kansas City Market などが登場しています

*3:式 5 にある出資というのはあるカテゴリの商品を需要 $\hat{V}_{i,c}$ の分だけ用意する際に必要となる費用等のことです

*4:この辺りの値はビジネスチームから提供されるようです

*5:この問題はポートフォリオ最適化問題として表現できます

*6:式 9c, 9d における季節成分 $\tau_{j,t}$ の表現方法は trigonometric seasonal model というもので，著者らが今回の使用している R の bsts パッケージに標準で用意されています

*7: $\hat{R}_m, \hat{I}_m, \hat{V}_m$ の詳細については論文内で明記されていませんが，恐らく先に登場した BSTS のモデルを使っているのではないかと思われます

*8:元の論文での記号の使い方に一部わかりにくい部分があったため，ここではすこし改変したものを表記しています

*9:line とは似た商品のグループを指します．例: プレーンヨーグルトとバニラヨーグルトは同じ line に属する

*10:ladder product とは同じアイテムでもパッケージサイズが大きいものを指します．例: 4 パック入のケチャップと 6 パック入のケチャップでは後者のほうが 1 つあたりの値段が安くなるように設定

*11:CausalImpact ではある介入(今回の場合は価格変更)を行わなかった場合の観測値を予測し，その予測値と実際の観測値を比較することで介入の効果の推定を行います．CausalImpact の概要に関してはこちらの動画が参考になります．より詳細を知りたい場合は元の論文の Brodersen et al. 2015，もしくは書籍の効果検証入門をご参照ください

*12:Figure 2 の original にある counterfactual prediction の線(青色の破線)が平坦になっていますが，これは需要予測モデルが週単位(考慮している季節成分のサイクルも週単位以上の長さ)に設定されていることに起因していると思われます

フレクトのクラウドblog re:newal

http://blog.flect.co.jp/cloud/からさらに引っ越しています