こんにちは.研究開発室の北村 蘭丸です.普段,研究開発室では Operations Research (OR) のビジネス活用について研究を進めています.その一環として,本記事では,Model Context Protocol (MCP) の仕組みを利用して Large Language Model (LLM) と OR の連携の仕方を模索するために,数理最適化を行うためのMCPサーバーを試作してみたのでご紹介いたします.簡単な問題であれば,会話のような自然なやり取りから数理最適化を行い結果を得るシステムの構築も可能なのではないかと考え,今回取り組んだことについてお話します.
1. はじめに
本記事では,普段から業務などで 数理最適化に取り組んでいる方々ではなく,数理最適化や意思決定に関わる AI について興味はあるが,その高いハードルにより一歩踏み出せずにいる専門家ではない方々を主なターゲットとしております.そのため,前者のような専門家の方々からすると,物足りない・厳密ではない・けしからんといった印象を抱かれるかもしれませんが,あくまでもこういった異なる技術領域の融合も含めた模索もあるのだなというスタンスでご覧いただければ幸いです.一方で,もしかしたら専門家の方々にとっても,数理最適化をより多くのユースケースに適用していくための新たなアプローチとして興味を持っていただけるかもしれません.
2. 数理最適化の活用に至るまでのハードル
数理最適化は様々な分野で活用されている技術ですが,その一方で,実際に日々の生活や業務で活用するためにはいくつかのハードルがあります.以下はその一例です.
そもそも数理最適化を知らない: 数理最適化という概念は一般の人にはほとんど浸透していないのが現状です.実際,日々の生活におけるさまざまな場面で恩恵を受けているはずですが,それを理解している人はそう多くないと考えられます.
実装するために知識と技術が必要: 仮に数理最適化という名前や概念くらいは知っていても,数理モデルを構築したり,汎用ソルバーなどを用いて実装するためには一定以上の知識と経験が必要になります.
ヒアリングが必要: 数理最適化モデルを作るためには,ドメイン知識が必要です.往々にして数理最適化の専門家がドメインの専門家に繰り返しヒアリングを行いながらモデルを構築することになります.このようにお互いに密な連携が必要となることもハードルをあげる要因になります.
モデルへの入力データが必要: 数理最適化モデルによって求解するためには,実問題を特徴付けるデータが必要になります.しかし,あまりにも膨大な量のデータを手動で入力しなければならないような場合,例えば,製造機器に関わるJob-shopスケジューリング問題を扱う際に,対象となる機器が数百台あり個々のパラメータが別に十数個あるとすると,パラメータ総数は数千のオーダーになってしまい,数理最適化を活用するハードルは上がってしまいます.このような場合には何らかの方法で人手の入力を極力減らさなければなりません.
3. 数理最適化のための MCP サーバーの試作
前述したような数理最適化の活用における最初のハードルを乗り越えるため,ここでは生成 AI,特に LLM の適用を検討してみたいと思います.近年,LLM を用いた Agentic な AI システムやサービスがドンドン出てきているわけですが,領域を絞ればかなり実用的な段階に入っていることは確かだと思います.こうしたモチベーションのもとで LLM の適用について考えてみたいと思います.
例えば,LLM がドメインの専門家にヒアリングの補助などを行ってくれると,一気にハードルは下がり,数理最適化のコモディティ化が進むのではないかなどと考えています.今回は,ユーザーと LLM (with MCP) 間でやり取りが完結するようなユースケースについて検討してみます.
3.1. Model Context Protocol (MCP) とは
2024 年 11 月に Anthropic により発表された,生成 AI アプリケーションと外部データソースやツールとの間でシームレスな統合を可能にするオープンプロトコルです.公式ドキュメントでは MCP を「AI 界の USB-C ポート」と喩えています.これは,まさに USB-C が様々な端子規格が乱立していたスマートフォンなどのデジタル機器を統一しつつあるように,MCP によって生成 AI モデルと様々なデータソースやツール規格の統一を目指していることを表しています.詳しくは公式ドキュメントなどを参照してください.
3.2. 試作した MCP サーバーについて
今回は図1に示すような使用方法を想定してMCP サーバーを構築しました.
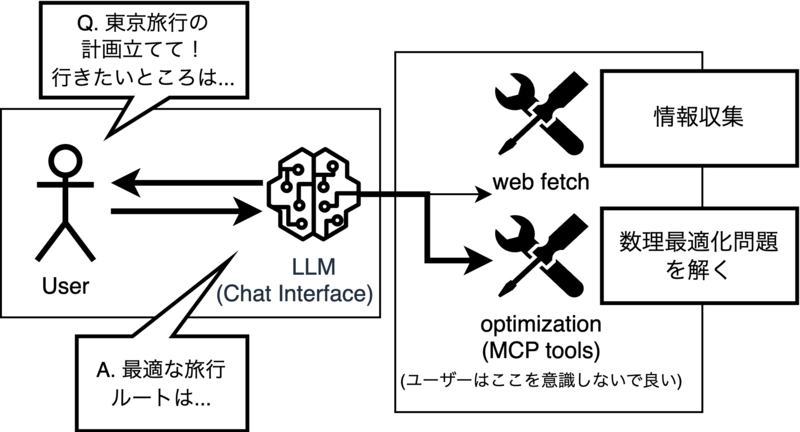
これを実現するために図2に示すようなプログラムを試作しました.
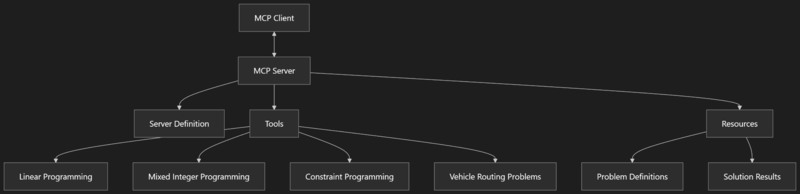
図を見てもらうとわかるように,今後の拡張を考えていくつかのコンポーネントを用意してあります.記事執筆現在はLP, MIPにしか対応しておりません.また,バックエンドとなる汎用ソルバーとしてはGoogle OR-Toolsを介してSCIP,GLOPを用いています.
▼ MCP サーバー定義の抜粋 [クリックで展開]
server: FastMCP = FastMCP(
name="optimization-server",
instructions="An MCP server for mathematical optimization problems. Can solve Linear Programming (LP) and Mixed Integer Programming (MIP) problems. ...",
)
server.add_tool(
fn=solve_optimization_problem,
name="solve_optimization_problem",
description="""Tool to solve optimization problems including Linear and Integer Programming (LP and MIP).
This tool provides a convenient way to solve various optimization problems using the power of
mathematical programming techniques. It supports both LP (continuous variables) and MIP (with integer/binary variables).
(以下省略)...
""",
)
server.run(transport="stdio")
サーバーの定義には FastMCP を利用しています.詳しい使い方については公式ドキュメントを参照いただければと思います.
▼ tools定義の抜粋 [クリックで展開]
async def solve_optimization_problem( params_input: OptimizationParams, ) -> dict[str, Any]: try: # Extract parameters from input model params: dict[str, Any] = params_input.params # Validate parameters logger.info("Validating Mathematical Programming problem parameters...") problem: MathematicalProgrammingProblem = ( MathematicalProgrammingProblem.model_validate(params) ) # Log problem type if problem.is_linear_problem(): logger.info( "Detected Linear Programming problem (no integer or binary variables)" ) else: logger.info( f"Detected Mixed Integer Programming problem with " f"{len(problem.integer_vars)} integer variables and " f"{len(problem.binary_vars)} binary variables" ) # Choose solver based on problem type if problem.is_linear_problem(): # For Linear Programming problems, use GLOP solver logger.info("Creating GLOP solver for Linear Programming...") solver: Solver = Solver.CreateSolver("GLOP") else: # For Mixed Integer Programming problems, use SCIP solver logger.info("Creating SCIP solver for Mixed Integer Programming...") solver: Solver = Solver.CreateSolver("SCIP") if not solver: raise RuntimeError( "Could not create solver. Please verify OR-Tools is correctly installed." ) # Create variables variables: dict[str, Variable] = create_variables(solver, problem) # Add constraints add_constraints(solver, problem, variables) # Set objective function set_objective(solver, problem, variables) # Execute optimization logger.info("Solving optimization problem...") start_time: float = time.time() status: int = solver.Solve() end_time: float = time.time() solve_time_ms: int = int((end_time - start_time) * 1000) # Process results logger.info(f"Solution complete. Status: {status}, Time: {solve_time_ms}ms") solution: MathematicalProgrammingSolution = process_solution( solver, status, variables, solve_time_ms ) # Return result as dictionary return solution.model_dump() except Exception as e: logger.error( f"Error occurred while solving optimization problem: {str(e)}", exc_info=True, ) # Create solution model with error information error_solution: MathematicalProgrammingSolution = ( MathematicalProgrammingSolution( status=SolutionStatus(code=-1, name="error", message=str(e)), solve_time_ms=0, ) ) return error_solution.model_dump()
tools本体の定義はこのようになっております.ただ順番に変数,制約条件,目的関数をセットしていって,最後に求解という流れになっています.また,入力データはPydanticでデータモデルを作って管理をしています.こちらも特別なことをしているわけではないため,詳しい使い方は公式ドキュメント (OR-Tools,Pydantic)に譲りたいと思います.
4. 簡単なユースケースによる検証
ここでは VS Code の拡張機能である Roo Code をユーザー側のインターフェースとして,東京旅行の計画を立ててもらうことにします.Roo Code については公式ドキュメントなどをご覧ください.今回は他にウェブ検索のために brave-search,fetch の MCP サーバーも別で導入しておいて,できるだけ外部の情報を参照しながら計画を練ってもらいます.
使用モデルはclaude-3.7-sonnet-20250219:thinkingです.ユーザーからのお願いは
『今から東京に遊びに行くんだけど、1日目は東京タワー、原宿、浅草あたり行きたい、夜は浅草のホテルに戻る。2日目は実物大のガンダムと、アキバでジャンクのPCパーツ漁り、あとはどっかおすすめのカレー屋でご飯食べて、夜はホテル戻りたい。3日目は18時の新幹線に送れないように東京駅周辺のスポットいくつか巡りたい。すでに動いてるMCPサーバーがあるはずなので、それ利用してウェブでおすすめスポット検索(brave-searchとfetch)して、その住所をもとにして、最適化(optimization-server)で最適な巡り順を考えて。時間はある程度任せる。』
と,思いつきで喋っているような,あえて雑な感じにしてみました.実際,『送れないように』はユーザーである私のタイプミスです...このくらいのフランクな文体で構造化されていない指示でも LLM が上手く (誤字なども吸収しつつ) ユーザーの抱いている要件を上手く汲み取れるかどうかがポイントです.一方,MCP の使用をやや強制するような指示にもしています.というのも,このようなツールの使用を指示をしない場合,ウェブ検索などを利用せずに LLM 自身の知識のみで回答しようとしてしまうためです.
4.1. 情報収集フェーズ
こちらから指定した通りにウェブ検索を活用して情報を収集してくれています.
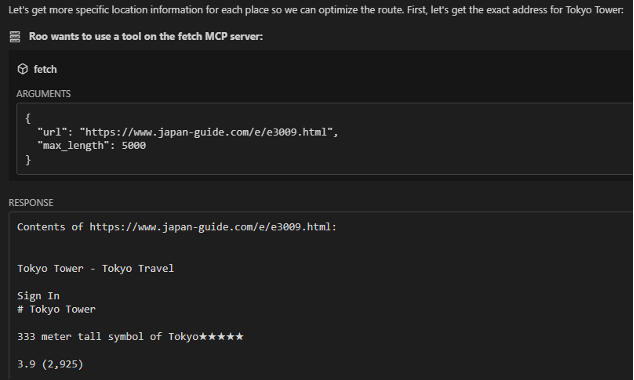
応答を見る限り確かに例示したスポットの情報はたくさん集めてくれているようですが,若干,指示に忠実すぎる傾向が見られました.雑談しつつオススメ情報をざっくばらんに引き出すのは難しそうです.ここでは省略しますが,こういうユースケースの場合,できるだけ周辺情報も考慮するようにしたり,LLM自身の知識をできるだけ信用しないようなチューニングやプロンプト設計が必要になるかもしれません.
4.2. 計画立案フェーズ
さて,本題の数理最適化のフェーズになります.今回のユースケースは,いわゆる Traveling Salesman Problem (TSP) などに帰着できるような問題設定です.今回は検証のために明示的に出発地点に戻ってくるなどの要件は伝えておらず,上手く LLM が空気を読んで補完してくれることを期待しています.初日や最終日は微妙かもしれませんが,少なくとも中日である2日目はホテルから出発してホテルに戻ってくることを前提に問題を立てて欲しいですね.
以降では特にポイントとなりそうなところにのみ絞って数理モデルを表す JSON と MCP サーバーから返ってきた解を見ていきます.
4.2.1. 1日目の計画立案
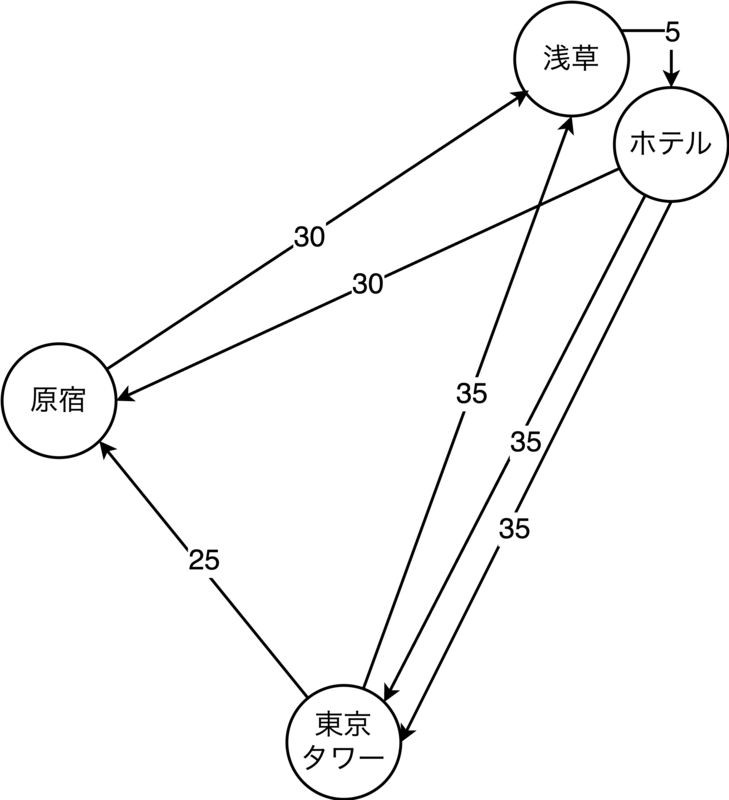
▼ 1日目の計画立案に使用されたJSON [クリックで展開]
{ "params_input": { "params": { "objective": { "coefficients": { "tokyo_tower_to_harajuku": 25, "harajuku_to_asakusa": 30, "asakusa_to_hotel": 5, "hotel_to_tokyo_tower": 35, "hotel_to_harajuku": 30, "tokyo_tower_to_asakusa": 35 }, "direction": "minimize" }, "constraints": [ { "name": "visit_tokyo_tower", "coefficients": { "tokyo_tower_to_harajuku": 1, "tokyo_tower_to_asakusa": 1, "hotel_to_tokyo_tower": 1 }, "lb": 1, "ub": 1 }, { "name": "visit_harajuku", "coefficients": { "tokyo_tower_to_harajuku": 1, "harajuku_to_asakusa": 1, "hotel_to_harajuku": 1 }, "lb": 1, "ub": 1 }, { "name": "visit_asakusa", "coefficients": { "harajuku_to_asakusa": 1, "tokyo_tower_to_asakusa": 1 }, "lb": 1, "ub": 1 }, { "name": "end_at_hotel", "coefficients": { "asakusa_to_hotel": 1 }, "lb": 1, "ub": 1 }, { "name": "start_from_hotel", "coefficients": { "hotel_to_tokyo_tower": 1, "hotel_to_harajuku": 1 }, "lb": 1, "ub": 1 } ], "binary_vars": [ "tokyo_tower_to_harajuku", "harajuku_to_asakusa", "asakusa_to_hotel", "hotel_to_tokyo_tower", "hotel_to_harajuku", "tokyo_tower_to_asakusa" ] } } }
▼ 返ってきた解 [クリックで展開]
{ "status": { "code": 0, "name": "optimal", "message": "Optimal solution found" }, "objective_value": 70.0, "variables": { "harajuku_to_asakusa": 1.0, "tokyo_tower_to_harajuku": -0.0, "hotel_to_tokyo_tower": 1.0, "asakusa_to_hotel": 1.0, "tokyo_tower_to_asakusa": 0.0, "hotel_to_harajuku": -0.0 }, "solve_time_ms": 0 }
割とストレートな表現の数理モデルを構築してきました.一つ一つの変数がある地点からある地点までの経路を表しており,今回はharajuku_to_asakusa,hotel_to_tokyo_tower,asakusa_to_hotelの3変数が選択されたようです.
一方で,良く見ていくとちょっと気になる点も見えてきます.ここでは「一度しか訪れない」という要件はこれで表現できているようですが,最初にホテルから出発するのか,東京駅に到着するのか,そのあたりの考慮ができていないように見受けられます.今回そもそもユーザーはどこを始点とするか指定していませんが,普通,我々がこういう問題設定で定式化を考えるときは,例えば TSP like (良く知られた抽象的な問題クラスの形) にモデリングできないか検討するのが常套手段のように思います.
また,浅草からホテルまでは5分となっているようですが,そうなると原宿から浅草まで30分なのと,ホテルから原宿まで30分という非対称性はどう考えれば良いのでしょうか?もしかしたら浅草駅からホテルは5分圏内みたいなことを暗に仮定しているのかもしれませんが,ホテルと浅草を同一視するか別の地点としてカウントするかが曖昧になっているように見えます.
いずれにせよ,できればこういうところは随時ユーザーの側に確認を入れて欲しいところです.
4.2.2. 2日目の計画立案
▼ 2日目の計画立案に使用されたJSON [クリックで展開]
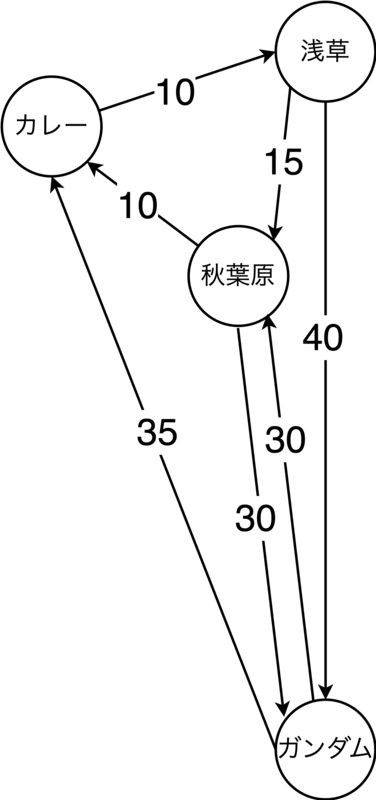
{ "params_input": { "params": { "objective": { "coefficients": { "hotel_to_gundam": 40, "hotel_to_akihabara": 15, "gundam_to_akihabara": 30, "gundam_to_curry": 35, "akihabara_to_curry": 10, "akihabara_to_hotel": 15, "curry_to_hotel": 10 }, "direction": "minimize" }, "constraints": [ { "name": "visit_gundam", "coefficients": { "hotel_to_gundam": 1, "gundam_to_akihabara": 1, "gundam_to_curry": 1 }, "lb": 1, "ub": 1 }, { "name": "visit_akihabara", "coefficients": { "hotel_to_akihabara": 1, "gundam_to_akihabara": 1, "akihabara_to_curry": 1, "akihabara_to_hotel": 1 }, "lb": 1, "ub": 1 }, { "name": "visit_curry", "coefficients": { "gundam_to_curry": 1, "akihabara_to_curry": 1, "curry_to_hotel": 1 }, "lb": 1, "ub": 1 }, { "name": "end_at_hotel", "coefficients": { "akihabara_to_hotel": 1, "curry_to_hotel": 1 }, "lb": 1, "ub": 1 }, { "name": "start_from_hotel", "coefficients": { "hotel_to_gundam": 1, "hotel_to_akihabara": 1 }, "lb": 1, "ub": 1 } ], "binary_vars": [ "hotel_to_gundam", "hotel_to_akihabara", "gundam_to_akihabara", "gundam_to_curry", "akihabara_to_curry", "akihabara_to_hotel", "curry_to_hotel" ] } } }
▼ 返ってきた解 [クリックで展開]
{ "status": { "code": 2, "name": "infeasible", "message": "No feasible solution exists" }, "objective_value": null, "variables": null, "solve_time_ms": 0 }
実行可能解が見つからない (infeasible) になったみたいです.LLM はこれをどうするのか見ていると,別のアプローチを考えるようです.
▼ LLMの返答 [クリックで展開]
It seems my optimization model for Day 2 has a feasibility issue. Let me think about why:
The constraints I set up might be conflicting. Let's look at what might be going wrong:
I'm trying to force the route to start from the hotel (either to Gundam or Akihabara) I'm requiring visits to Gundam, Akihabara, and a curry restaurant I'm requiring an end at the hotel (either from Akihabara or the curry place) There might be a connectivity issue where the model can't find a valid path that satisfies all constraints. The issue could be related to flow conservation - each location needs to have balanced inflow and outflow.
Let me try a different approach for Day 2. Instead of using binary variables for each segment, I'll use a simpler ordering approach:
(訳) 私の2日目の最適化モデルには実現可能性の問題があるようです。その理由を考えてみます:
私が設定した制約が矛盾しているのかもしれません。何が間違っているのか見てみましょう:
ルートを強制的にホテルからスタートさせようとしている(ガンダムか秋葉原) ガンダム、秋葉原、カレー屋を訪問することを要求している ホテルで終了することを要求している(秋葉原かカレー屋から) モデルがすべての制約を満たす有効なパスを見つけられないという接続性の問題があるかもしれません。この問題は、フローの保全に関連している可能性があります。各ロケーションは、流入と流出のバランスがとれている必要があります。
2日目は別のアプローチを試してみます。各セグメントにバイナリ変数を使用する代わりに、より単純な順序付けアプローチを使用します:
モデルの方を見てみると,例えばvisit_gundam制約で,ガンダムに向かう経路とガンダムから別の場所へ向かう経路の合計が1本という意味になってしまっています.その他の制約も似たような感じになっており,モデルが上手く問題を表現できていません.これについて LLM はフロー制約に類する制約条件が必要かもしれないと気づいたようです.
▼ 2日目の計画立案に使用されたJSON (リトライ版) [クリックで展開]
{ "params_input": { "params": { "objective": { "coefficients": { "hotel_to_gundam": 40, "hotel_to_akihabara": 15, "gundam_to_akihabara": 30, "akihabara_to_gundam": 30, "akihabara_to_curry": 10, "gundam_to_curry": 35, "curry_to_hotel": 10 }, "direction": "minimize" }, "constraints": [ { "name": "one_route_from_hotel", "coefficients": { "hotel_to_gundam": 1, "hotel_to_akihabara": 1 }, "lb": 1, "ub": 1 }, { "name": "one_route_to_gundam", "coefficients": { "hotel_to_gundam": 1, "akihabara_to_gundam": 1 }, "lb": 1, "ub": 1 }, { "name": "one_route_from_gundam", "coefficients": { "gundam_to_akihabara": 1, "gundam_to_curry": 1 }, "lb": 1, "ub": 1 }, { "name": "one_route_to_akihabara", "coefficients": { "hotel_to_akihabara": 1, "gundam_to_akihabara": 1 }, "lb": 1, "ub": 1 }, { "name": "one_route_from_akihabara", "coefficients": { "akihabara_to_gundam": 1, "akihabara_to_curry": 1 }, "lb": 1, "ub": 1 }, { "name": "one_route_to_curry", "coefficients": { "akihabara_to_curry": 1, "gundam_to_curry": 1 }, "lb": 1, "ub": 1 }, { "name": "one_route_from_curry", "coefficients": { "curry_to_hotel": 1 }, "lb": 1, "ub": 1 } ], "binary_vars": [ "hotel_to_gundam", "hotel_to_akihabara", "gundam_to_akihabara", "akihabara_to_gundam", "akihabara_to_curry", "gundam_to_curry", "curry_to_hotel" ] } } }
▼ 返ってきた解 (リトライ版) [クリックで展開]
{ "status": { "code": 0, "name": "optimal", "message": "Optimal solution found" }, "objective_value": 90.0, "variables": { "akihabara_to_gundam": 0.0, "akihabara_to_curry": 1.0, "hotel_to_gundam": 1.0, "hotel_to_akihabara": 0.0, "curry_to_hotel": 1.0, "gundam_to_akihabara": 1.0, "gundam_to_curry": -0.0 }, "solve_time_ms": 0 }
今度は LLM が意図した (と思われる) 形の解が返ってきているようですね.
4.2.3. 3日目の計画立案
▼ 3日目の計画立案に使用されたJSON [クリックで展開]
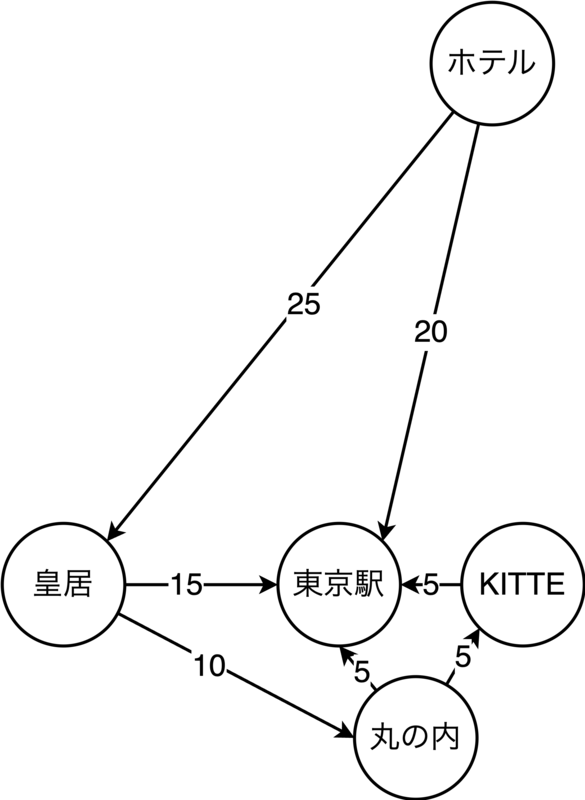
{ "params_input": { "params": { "objective": { "coefficients": { "hotel_to_imperial_palace": 25, "hotel_to_tokyo_station": 20, "imperial_palace_to_marunouchi": 10, "imperial_palace_to_tokyo_station": 15, "marunouchi_to_kitte": 5, "marunouchi_to_tokyo_station": 5, "kitte_to_tokyo_station": 5 }, "direction": "minimize" }, "constraints": [ { "name": "one_route_from_hotel", "coefficients": { "hotel_to_imperial_palace": 1, "hotel_to_tokyo_station": 1 }, "lb": 1, "ub": 1 }, { "name": "visit_imperial_palace", "coefficients": { "hotel_to_imperial_palace": 1, "imperial_palace_to_marunouchi": 1, "imperial_palace_to_tokyo_station": 1 }, "lb": 1, "ub": 1 }, { "name": "one_route_from_imperial", "coefficients": { "imperial_palace_to_marunouchi": 1, "imperial_palace_to_tokyo_station": 1 }, "lb": 1, "ub": 1 }, { "name": "visit_marunouchi", "coefficients": { "imperial_palace_to_marunouchi": 1, "marunouchi_to_kitte": 1, "marunouchi_to_tokyo_station": 1 }, "lb": 0, "ub": 1 }, { "name": "one_route_from_marunouchi", "coefficients": { "marunouchi_to_kitte": 1, "marunouchi_to_tokyo_station": 1 }, "lb": 0, "ub": 1 }, { "name": "visit_kitte", "coefficients": { "marunouchi_to_kitte": 1, "kitte_to_tokyo_station": 1 }, "lb": 0, "ub": 1 }, { "name": "end_at_tokyo_station", "coefficients": { "hotel_to_tokyo_station": 1, "imperial_palace_to_tokyo_station": 1, "marunouchi_to_tokyo_station": 1, "kitte_to_tokyo_station": 1 }, "lb": 1, "ub": 1 } ], "binary_vars": [ "hotel_to_imperial_palace", "hotel_to_tokyo_station", "imperial_palace_to_marunouchi", "imperial_palace_to_tokyo_station", "marunouchi_to_kitte", "marunouchi_to_tokyo_station", "kitte_to_tokyo_station" ] } } }
▼ 返ってきた解 [クリックで展開]
{ "status": { "code": 0, "name": "optimal", "message": "Optimal solution found" }, "objective_value": 30.0, "variables": { "kitte_to_tokyo_station": -0.0, "marunouchi_to_kitte": -0.0, "hotel_to_imperial_palace": 0.0, "marunouchi_to_tokyo_station": -0.0, "imperial_palace_to_tokyo_station": 0.0, "imperial_palace_to_marunouchi": 1.0, "hotel_to_tokyo_station": 1.0 }, "solve_time_ms": 0 }
3日目はあえてスポットを指定せずにオススメを聞く形にしました.東京駅周辺のスポットを巡るということで,皇居やKITTEなどが候補に挙がっています.
これまでのモデルが出力した JSON の特徴をまとめてみます.まず,概ねできていると言って良いところは以下となるでしょう.
- 変数を経路に対応付けることはできている
- 目的関数には移動時間を対応付けている
一方で,できていない点は以下となります.
- ユーザーから追加の情報を聞き出せていない
- 不完全な制約条件になっていることがある
- 変数は各地点について網羅的ではない
- 本来訪れるべき経路が選択できていない
必要に応じてユーザーから追加の情報を聞き出せていないことについてですが,例えばこちらの記事などで言及されているように,いわばロールプレイングなどの形式を指示するなど,ヒアリングタスクに向けて調整されたプロンプトを渡すことで改善可能ではないかと考えています.
フロー制約などが不完全なのは,根本的に上手く要件を数理モデルに落とし込めていないことになります.会話っぽく曖昧な指示によって,いわゆる「数理最適化」っぽいコンテキストになりきらなかったのも要因としてありそうです.また,細かい点を挙げるとキリがないのですが,例えば訪れたいスポットの数や移動時間が1日に収まりきらない場合の考慮や,滞在時間についての考慮が全くなされていないことについても,やはり改善が必要だと思います.
変数が網羅的でない部分について,ホテルからは出る経路が大抵複数あるのに対し,帰ってくる経路は1本しかない,という点に注目してみます.単なる間違いや出力の質の問題とも考えられますが,一方で,LLM が持ついわば「常識」によって,変数の削減が行われた結果ではないかとも考えられます.これは数理モデルを小さくできるので嬉しい反面,例えば常識では考えつかないような裏道的な経路があった場合に,その解に辿り着くことができなくなってしまうという側面もあります.つまり,本来の数理最適化モデルの持つ網羅性やシミュレーター的な側面が失われてしまうということです.いずれにせよ,もし「常識による変数の削減」であるならば大変興味深い現象です.
4.3. 最終出力
参考までに最終的な出力も載せておきます.
▼ 東京3日間の旅程 [クリックで展開]
1日目:東京タワー、原宿、浅草
午前:
9:00: 浅草のホテルからスタート
浅草線で神谷町駅へ(約25~30分)
10:00 - 12:00: 東京タワー(高さ333m)
住所: 東京都心部、御成門・赤羽橋・神谷町駅近く
入場料:1,500円(メインデッキ)または3,500円(両デッキ)
150mの展望デッキで街の景色を楽しむ
午後:
12:30 日比谷線で恵比寿へ、JR山手線で原宿へ(約25分)
13:00 - 15:30: 原宿散策
竹下通り(ファッション・ブティックが軒を連ねる350mのショッピング・ストリート)
住所: 渋谷区神宮前 1 丁目
有名なクレープやレインボー綿菓子を食べたり、個性的なファッション・ショップを巡る
夕方:
16:00: JR山手線で上野へ、銀座線に乗り換えて浅草へ(約30分)
16:30 - 19:00: 浅草散策
浅草寺(東京最古の仏教寺院)
仲見世商店街(伝統的なお土産が並ぶ 250m の通り)
浅草神社
19:00: 夜は浅草のホテルに戻る
2日目: ガンダム像、秋葉原、カレー
午前:
9:00: 浅草のホテルからスタート
浅草線で新橋、ゆりかもめで台場へ(約40分)
10:00 - 12:00: 実物大ユニコーンガンダム立像見学
場所: お台場・ダイバーシティ東京プラザ2F フェスティバルプラザ
AM11:00から変身ショーを鑑賞
7FのTHE GUNDAM BASE TOKYO(ガンプラ公式施設)を探検
午後:
12:30: ゆりかもめで新橋、JRで秋葉原へ(約30分)
13:00 - 16:00: 秋葉原でジャンクPCパーツを探す
ツクモパソコン本店(千代田区外神田1-9-7)
営業時間: 10:00 - 22:00
秋葉原ジャンクストリートで中古パーツもチェック
夕方:
16:30 - 18:00: カレー屋で夕食
オススメ: 肉の万世(朴葉カレーの店)、秋葉原の便利な場所にある
代替案: カレーステーション・ナイアガラ(ミニチュア列車がカレーを運ぶ)
18:30: 浅草のホテルに戻る(つくばエクスプレスまたは銀座線で15分)
3日目:東京駅と皇居
午前:
10:00: 浅草ホテルをチェックアウト(必要に応じて荷物を預ける)
銀座線で東京駅へ(約20分)
10:30 - 12:30: 東京駅周辺を散策
ヨーロッパ建築の歴史ある東京駅舎
丸ビルやKITTEモールでショッピング
午後:
12:30 - 13:30: 東京駅でのランチ
駅構内の「キッチンストリート」には多くのレストランがあります
14:00 - 16:00: 皇居・庭園見学
東京駅から徒歩(約15分)
庭園や史跡を散策
美しいお堀のある皇居の写真を撮る
夕方:
16:30 - 17:30: 東京駅に戻り、荷物を受け取る(保管されている場合)
東京キャラクターストリートを見学、または新幹線に乗るためのお弁当を購入
18:00: 新幹線に乗車(出発の15分前までにホームに到着)
交通機関の注意事項:
移動に便利なPASMO/Suicaカードの購入を検討
最適化により、このルートは場所間の移動時間を最短にしている
タクシーは利用できるが高い
地下鉄/JRシステムは効率的
東京への旅をお楽しみください!
5. まとめ
本記事では,数理最適化を活用するハードルを下げることができそうな技術領域として LLM に注目し,連携方法を模索するため MCP サーバーを試作し,定性的ではありますが簡単なユースケースで検証を行いました.
日常会話のようなフランクな指示を試してみることで,LLM をインターフェースとした OR 活用の可能性を垣間見ることができました.また,LLM の持つ常識による変数削減とも捉えられるような現象も観察されました.一方で,LLM の出力をそのまま数理最適化に使うのはやはり難しく,MCP サーバー,LLM への指示の出し方なども含め,この掛け合わせ方には工夫や改善の余地がありそうです.
最後までお読みいただきありがとうございます.Flect では今後もお客様にとって付加価値となるような新たな分野や技術に関して開拓を行っていきます.今回ご紹介したような LLM に関する取り組み以外にも,業務上の意思決定に関したその他の AI や OR の研究を行っておりますので,ご興味がありましたら是非ご相談ください.
Appendix: 補足
ありがたいことに,いくつかSNSなどで反応をいただいているようで恐縮です.また,その中でご指摘いただいている点について (ご指摘に関しては本当におっしゃる通りです) 少し補足させてください.
ご覧いただいた通り,本記事では簡単な指示の上で LLM とユーザーのやり取りで完結するようなユースケースを考えたわけですが,(繰り返しになりますが) ここで LLM が出力した数理最適化モデルはどれも間違っています.そこから得られる示唆について,今後も継続して検討すべきところと思われます.
今回は数理最適化モデルを考えさせる部分も LLM に任せたわけですが,例えば別の境界の切り方として,より specific な問題設定ごとに tools を用意しておくといった方法もあると考えています.このようにすることで,LLM が考えるのは「この問題は tools のうちどれに対応するか?」の部分になり,数理モデルを1から考えさせなくても良くなります.これについては,過去の取り組みの一部が流用可能ではないかとも考えていたりします.
いずれにせよ,本記事はあくまでもこのようなユースケースに対して,ユーザー側・開発者側共に,特別な工夫なしでどこまでやれるのか検討する意味合いが強いです.この点に関してはご了承いただければと思います.補足含め,最後までお読みいただきありがとうございました.